We all know what a circle is, but what are the principles that govern why an object moves in circles?
How do we discuss its motion when it travels in a circle? In the series of lessons which involves kinematics and dynamics, we will discuss what circular motion is, how it's measured, some complex examples of circular motion, and the causes behind circular motion.
How do we discuss its motion when it travels in a circle? In the series of lessons which involves kinematics and dynamics, we will discuss what circular motion is, how it's measured, some complex examples of circular motion, and the causes behind circular motion.
|
In a rush? Need only a quick review? Watch this Otherwise continue on |
|
Understanding Circular Motion
|
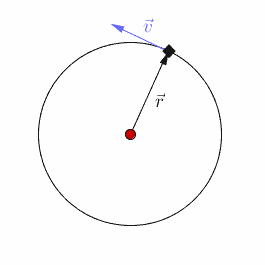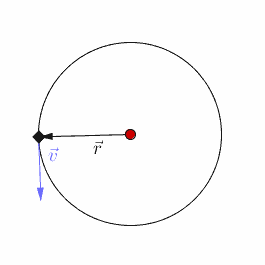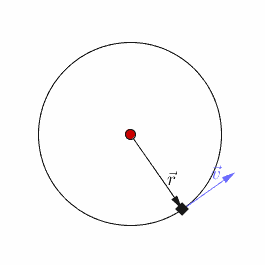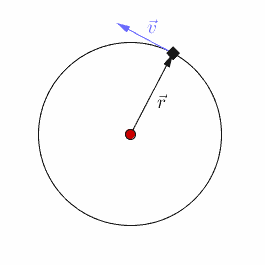
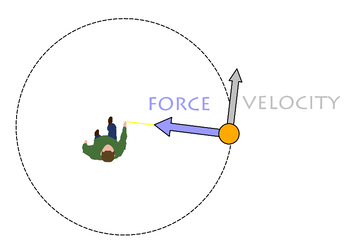
In this lesson we will examine the principles behind uniform circular motion. In other words, situations when the object undergoing circular motion is traveling at a constant speed.
The path has a constant radius (r) and a Period (T). However, the velocity is not constant. Although the magnitude of the velocity (which is the speed) is constant, its direction is constantly changing, since it is a vector. |
|
|
This leads to an important point.
Since the velocity is changing, it must be accelerating. Since it is accelerating, it must be experiencing a net force. It is this force, the centripetal force, that causes the object to undergoing circular motion. |
The following video explores this in greater detail, including the formulas involved in the analysis of circular motion
Check your understanding
Sample Problem
We are now ready to try some sample problems
Below are sample problems with videos that explain how to solve them. It is suggested you try the problems beforehand, as this actually aids understanding, even if you are unsure if you are correct.
We are now ready to try some sample problems
Below are sample problems with videos that explain how to solve them. It is suggested you try the problems beforehand, as this actually aids understanding, even if you are unsure if you are correct.
|
|
|
|
Here are some more problems to try out
- An ant is riding on the tip of a 10 cm long secondhand of o'clock. Find the linear velocity of the ant. (62 cm/s)
- Calculate the centripetal force required to keep a 5 kg mass revolving in a circular path of radius 125 cm with a period of two seconds. (61.9 N)
- An astronaut is on a spinning space station so that he experiences artificial gravity, just like the film space Odyssey 2001. If the radius of the station is 1000 m, what will be the tangential velocity? (99 m/s)
- As you go around the corner at 72 km/h you experience a force of 1120 N from the seat of your car. If your mass is 70 kg what is the radius of the curve? (25m)
- A centripetal force of 8.94 N is required to keep an object in a circular orbit. What is the mass of the object if it is travelling with a constant speed of 8.10 m/s and a radius of 5.29 m? (0.72 kg)
