Dynamics is a subset of mechanics, which is the study of motion. Whereas kinetics studies that motion itself, dynamics is concerned about the CAUSES of motion. In particular, it involves the concepts of force, momentum and energy. This video gives an overview of what dynamics is, and is useful as an intro to its study, or as a review
MOMENTUM
Momentum is intricately connected to the concept of force. In fact in Newton's Principia he described his second law of motion in terms of momentum.
In classical physics the concept of momentum is relatively straightforward. It's simply an object mass times its velocity.
In classical physics the concept of momentum is relatively straightforward. It's simply an object mass times its velocity.
momentum = mass x velocity
p = m x v
unit : kg.m/s
p = m x v
unit : kg.m/s
So for example a heavy moving object will have a large momentum due to its mass. But an object can also have a large momentum if it's velocity is particularly high. So for example a bullet can have a relatively large momentum by way of its velocity.
A Change in Momentum
The analysis of motion is more concerned why an object's motion changes,. In other words, it has a change in velocity, it accelerates
As a result, there is a change in momentum
A change in momentum is called its impulse.
The analysis of motion is more concerned why an object's motion changes,. In other words, it has a change in velocity, it accelerates
As a result, there is a change in momentum
A change in momentum is called its impulse.
|
|
Watch the video as I explain using the 'eggsample' of an egg falling (get it), as well as cars safety, the concepts of momentum and impulse. |
Check your understanding
Sample Problem
We are now ready to try a sample problem
Below is a sample problem with a video that explain how to solve it. It is suggested you try the problem beforehand, as this actually aids understanding, even if you are unsure if you are correct.
We are now ready to try a sample problem
Below is a sample problem with a video that explain how to solve it. It is suggested you try the problem beforehand, as this actually aids understanding, even if you are unsure if you are correct.
Here are some more problems for you to try. Answers are provided.
- Calculate the magnitude of the momentum in the following cases:
(a) a proton (mass = 1.67 x 10-27 kg)) moving with a speed of 5 x 106 ms-1, (8.35 x 10-21 Ns)
(b) a 15 g bullet moving at a speed of 500 ms-1,
(c) a 75 kg sprinter running at a speed of 12 ms-1,
(d) The earth (mass = 5.98 x 1024 kg) moving at an orbital speed of 2.98 x 104 m/s. - An 18,000 kg van is moving at a speed of 15 ms-1. If Superman is to stop the van in 0.5 s, what average force must he exert on the van? (-540,000 N)
- A 0.15-kg baseball is thrown at a speed of 20 ms-1. It is hit straight back at the pitcher with a final speed of 22 ms-1
(a) What impulse is delivered to the ball? (6.3 Ns towards pitcher)
(b) Find the average force exerted by the bat on the ball if the two are in contact for 2 x 10-3 s. (3,150 N towards pitcher)
Here another worksheet on impulse, includes answer - worked out solutions
CONSERVATION OF MOMENTUM
An important thing to consider is that when an object experiences a force and thus its momentum changes, the object that caused the force also experiences a force (consistent with the third law) and thus its momentum changes.
The net result is that if we determine the total momentum of all the objects in the system BEFORE they collide, it will equal the total momentum of the objects after they collide. We say the momentum is conserved.
This is called the Law of Conservation of Momentum, or in short, LCM.
The net result is that if we determine the total momentum of all the objects in the system BEFORE they collide, it will equal the total momentum of the objects after they collide. We say the momentum is conserved.
This is called the Law of Conservation of Momentum, or in short, LCM.
In the following video, using the crash between a bus and a bee I show how we derive and understand Conservation of Momentum
Interactive
Now its an opportunity to play.
Using the animation from pHET, start by exploring LCM rectilinearly, that is, in one dimension. click the intro TAB.
Leave the check off on kinetic energy and keep the elasticity to 100%
adjust the initial velocities ands then observe both the resulting collision but also examine the vector diagrams in the momenta diagram in the bottom right.
You can also do this in the Explore 1D TAB. You will note that total momentum of the system remains constant.
Since momentum is a vector quantity, the same is true for two dimension situations.
Once you are confident in one dimension, explore two dimensions. Again , the total momentum of the system remains constant, irrespective of the individual momenta of each individual object
Now its an opportunity to play.
Using the animation from pHET, start by exploring LCM rectilinearly, that is, in one dimension. click the intro TAB.
Leave the check off on kinetic energy and keep the elasticity to 100%
adjust the initial velocities ands then observe both the resulting collision but also examine the vector diagrams in the momenta diagram in the bottom right.
You can also do this in the Explore 1D TAB. You will note that total momentum of the system remains constant.
Since momentum is a vector quantity, the same is true for two dimension situations.
Once you are confident in one dimension, explore two dimensions. Again , the total momentum of the system remains constant, irrespective of the individual momenta of each individual object
Sample problems
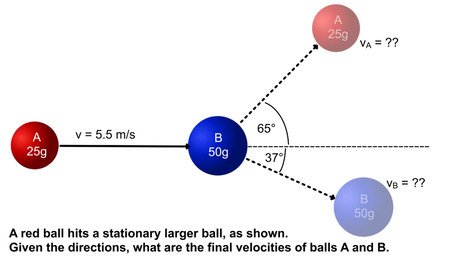
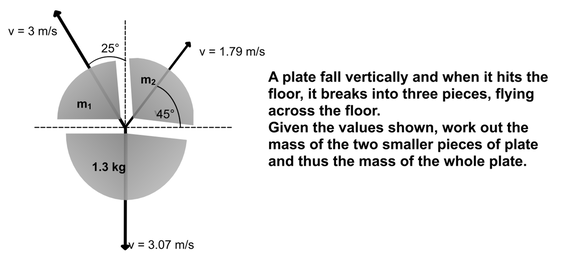
We now have three sample problems. The first in 1D, the second two are 2D
Have a go at each before watching video
We now have three sample problems. The first in 1D, the second two are 2D
Have a go at each before watching video
Here are some more problems to try
- A 40-kg child standing on a frozen pond throws a 0.5-kg stone to the east with a speed of 5 m/s. Find the recoil velocity of the child. (0.0625 m/s)
- A rifle with a weight of 30 N fires a 5-g bullet with a speed of 300 m/s. Find the recoil speed of the rifle, if it is held loosely by the shooter. (0.49 m/s)
- A 65-kg boy and a 40-kg girl, both wearing skates, face each other at rest on a skating rink. The boy pushes the girl, sending her to the east with a speed of 4 m/s. What is the velocity (speed and direction) of the boy? (2.46 m/s west)